エールフレットの時空理論が完成され、エールフレットの未解決問題が解決されました
今回、アリビナ宇宙科学研究所(AISU)の内部組織架空世界研究室(IWL)によって、エールフレットの未解決問題であった「エールフレットの時間問題」の解決が開始され、AISU-ETCS理論の完成をもってこの未解決問題が解決されました。
AISU-ETCS — エールフレット時空座標計算システムの理論的基盤
アリビナ宇宙科学研究所(AISU)は、架空世界エールフレットの時空構造を記述する数理的枠組みとして「Al'bina Institute Erflett Temporal-gravitational Calculation System(AISU-ETCS)」を開発しました。本稿では、このシステムの理論的基盤をご紹介します。
AISU-ETCSのコア: https://systems.belkosmos.com/etcs/
AISU-ETCS付属4つのシステム一覧: https://systems.belkosmos.com/time/
エールフレットの幾何学的構造
エールフレットの世界は、逆四角錐(ピラミッド)型の時空構造として数理的にモデル化されています。基準平面(高度 \(z = 0\) km)における対角線長は \(D_0 = 8{,}776.263\) km、頂点の深度は \(z_v = -4{,}739.857\) km、上面(基底面)の高度は \(z_b = +1{,}579.952\) km です。
任意の高度 \(z\) における断面の対角線長 \(D(z)\) は、頂点からの距離に比例して線形に拡大します: $$D(z) = D_0 \cdot \frac{z - z_v}{-z_v}$$
また、各高度における有効領域は、\(|x| + |y| \leq D(z)/2\) を満たすひし形(45°回転した正方形)の断面として定義されます。座標系は東西方向を \(x\) 軸、南北方向を \(y\) 軸、鉛直方向を \(z\) 軸とします。
X パラメータ — 時空結合強度
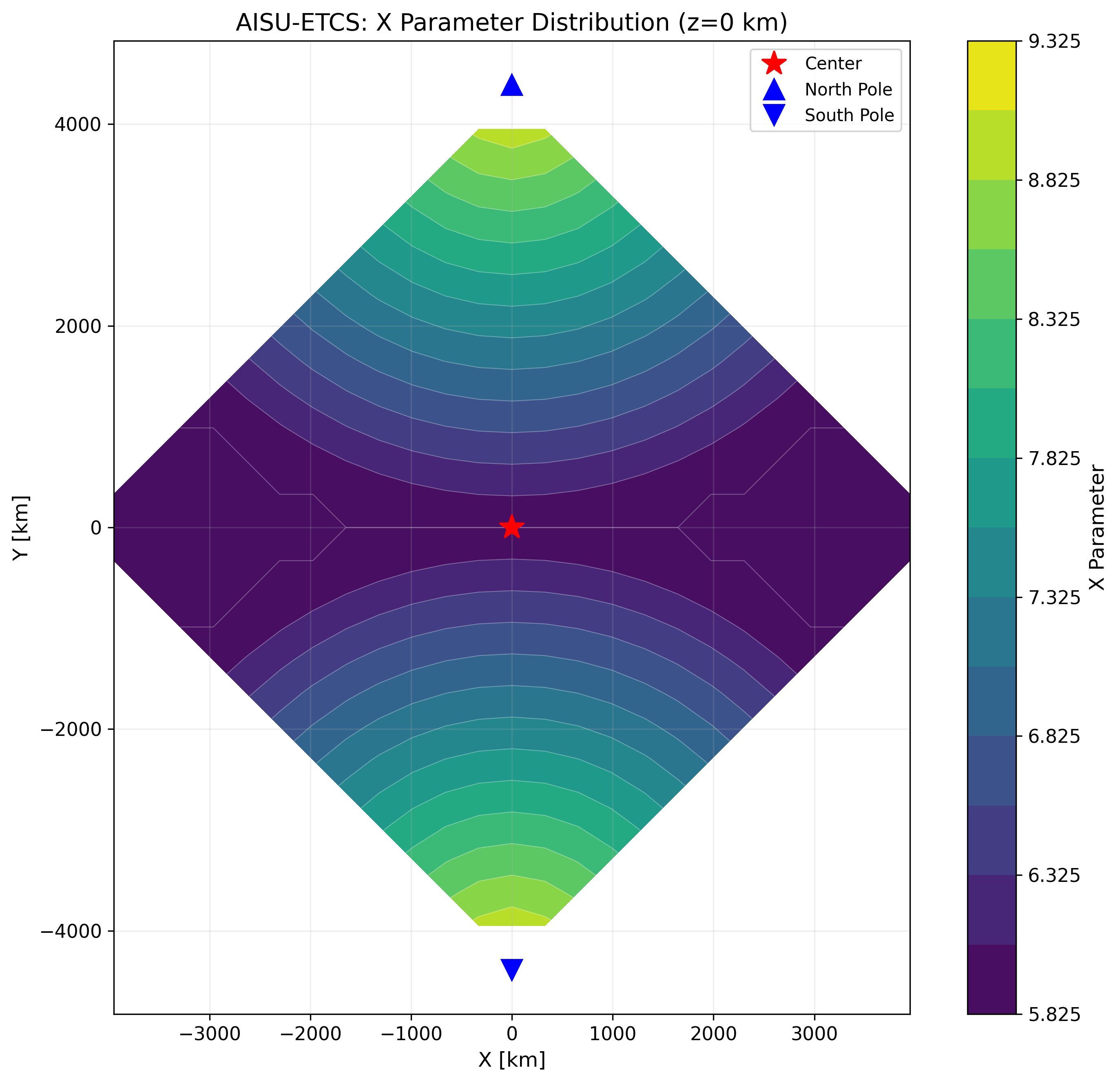
エールフレットの時空構造において中心的な役割を担うのが「X パラメータ」です。これは各地点における時間的・空間的結合の強さを表す無次元量であり、北極・南極(\(y\) 軸上の両端点)からの距離によって決まります。
X パラメータの値域は \(X_{\min} = 5.825\)(重心点)から \(X_{\max} = 9.325\)(北極・南極)であり、重心から極に向かうにつれて滑らかに増加します。さらに、エールフレットの時空歪曲周期「セイラット周期」(約 387.09 日)に応じた周期的な摂動が加わります: $$X_{\text{eff}} = X_{\text{geom}} \cdot \left(1 + \varepsilon \sin\!\left(\frac{2\pi D_F}{T_{\text{Theilaht}}}\right)\right)$$
ここで \(\varepsilon = 0.011236\)、\(D_F\) はフーリカ暦の通算日数です。
固有時間比 — 場所によって異なる時間の流れ
AISU-ETCS の最も重要な成果のひとつが、固有時間比 \(\tau_{\text{ratio}}\) の定式化です。これは、基準点(重心)における時間の流れを 1.0 としたとき、各地点での時間の進む速さを表す比率です: $$\frac{d\tau}{d\tau_0} = \tau_{\text{vertical}}(z) \cdot \tau_{\text{horizontal}}(X_{\text{eff}}, \phi)$$
垂直成分(高度依存)は、高度が上がるほど時間がわずかに速く進み(天界)、深部(晶界)では頂点に近づくにつれて時間がほぼ停止に近づきます。基準高度(\(z = 0\))では \(\tau_{\text{vertical}} = 1.0\) となります。
水平成分(南北非対称)は、フェーズ \(\phi\) によって決まります:
$$\tau_{\text{horizontal}} = \begin{cases} X_{\text{eff}} / X_{\min} & \phi = +1 \text{(北部:時間が速い)} \\ X_{\min}^3 / X_{\text{eff}}^2 & \phi = -1 \text{(南部:時間が遅い)} \\ 1 & \phi = 0 \text{(中軸:基準)} \end{cases}$$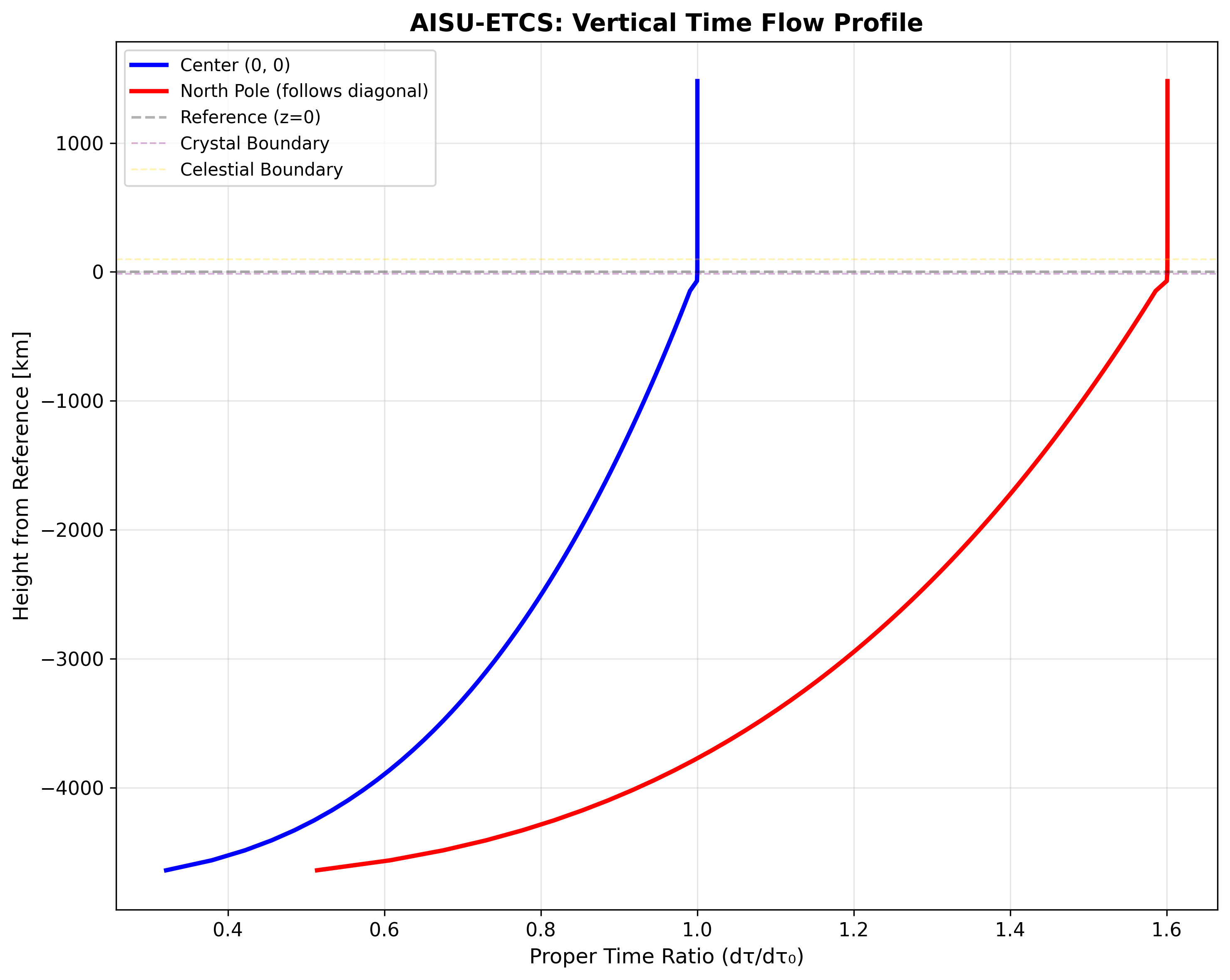
たとえば基準高度における北極点では \(\tau_{\text{ratio}} \approx 1.601\)(基準の約 1.6 倍の速さ)、南極点では \(\tau_{\text{ratio}} \approx 0.390\)(基準の約 0.39 倍の遅さ)となります。
力学的重力場
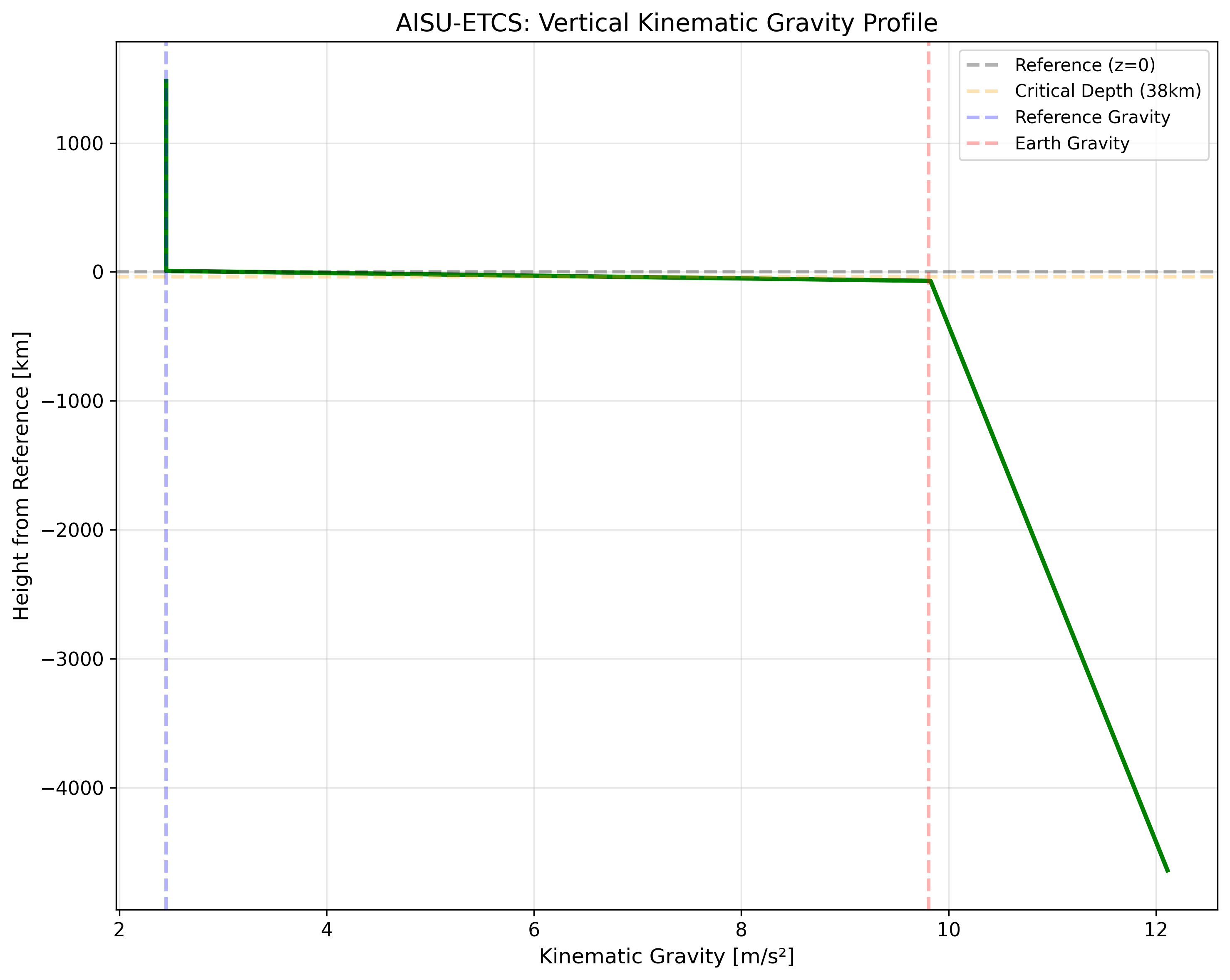
エールフレットにおける重力加速度は「力学的重力 \(g_k\)」として定義されます。これはニュートン力学的な質量引力ではなく、時空の曲率(固有時間の高度勾配)から生じる実効的な加速度です: $$g_k = -c^2 \frac{\partial \ln \tau_{\text{vertical}}}{\partial h}$$
基準高度での重力加速度は \(g_{\text{ref}} = 2.4525\) m/s²(地球の約 1/4)です。地下深部(晶界)では地球と同等の 9.81 m/s² 程度まで増大し、さらに深部では線形に増加します。
領域区分(レルム)
エールフレットの世界は高度に応じて三つの領域(レルム)に区分されます:
| レルム | 高度範囲 | 時間の流れ | 重力加速度 |
|---|---|---|---|
| 天界(Umyria Herra) | \(z > +96.82\) km | \(\tau > 1.0\)(速い) | \(g < 2.45\) m/s² |
| 永界(Erflett Herra) | \(-13.99 < z < +96.82\) km | \(\tau \approx 1.0\)(基準) | \(2.45 \sim 3\) m/s² |
| 晶界(Nivlkut Herra) | \(z < -13.99\) km | \(\tau < 1.0\)(遅い) | \(g > 3\) m/s² |
各レルム間の境界は連続的な遷移として定義されており、境界を越えても物理量は不連続に変化しません。
時間座標変換と ETM
エールフレットの標準時間単位は「ニムノー(nimneu, n)」であり、1 ニムノーは約 1.04167 秒に相当します。エールフレット全域の共通時刻座標「Erflett Temporal Mechanics(ETM)」と、各地点での固有時刻「Local Coordinate(LC)時刻」の変換は以下の式で行われます: $$n_{\text{LC}} = n_{\text{ETM}} \cdot \tau_{\text{ratio}}(x, y, z, D_F, \phi)$$
また、東西経線帯(ESM)による時差補正も組み込まれており、エールフレット内の地域時刻への変換も可能です。
計算システムと可視化ツール
AISU-ETCS は REST API として実装されており、任意の座標点における時空特性(固有時間比・運動学的重力・X パラメータ・レルム分類など)をリアルタイムで計算・取得できます。また、エールフレット時空ピラミッドの三次元可視化ツール「AISU-ETCS Spacetime Visualiser」も公開されており、任意の高度断面における各物理量の分布をインタラクティブに確認できます。
また地球時刻との変換を行う変換装置や、エールフレットの円盤時計も作成されました。
本システムの理論的詳細については、当研究所の技術文書「AISU-ETCS Mathematical Framework and Theoretical Foundations v2.0」をご参照ください。
